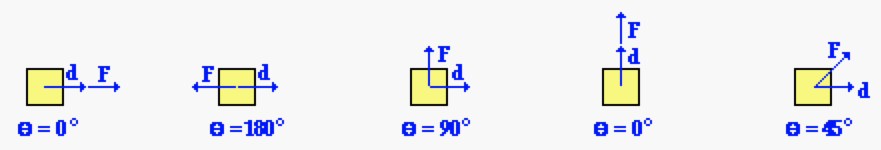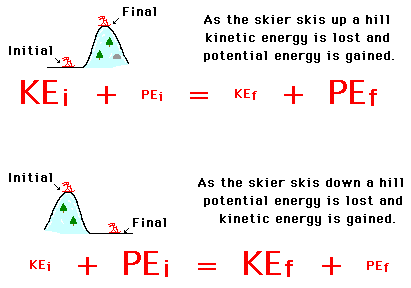Work Energy Principle Formula

It is also known as the principle of work and kinetic energy.

Work energy principle formula. In other words w is telling you the amount of energy that the force f is giving to the object. Potential energy kinetic energy work constant. The unit of power is watt w. Work and potential energy.

Work energy theorem states that. For pure rotation the net work is equal to the change in rotational kinetic energy. Mgh 0 5mv 2 force distance k. For a spring this can be written.

Power can be defined as the rate at which work is done i e. W refers to the work done by the force f. The formula for power is. If energy is not conserved then it is used to do work.

For the potential energy the formula is. This linear relationship between the force and the displacement is known as hooke s law. The si unit of energy is joules j which is named in honour of james prescott joule. F kx where k is known as the spring constant.

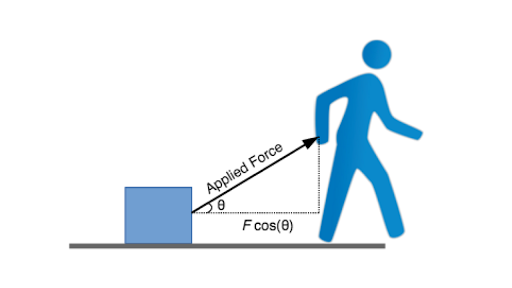
The work energy principleis a general principle which can be applied specifically to rotating objects. The formula to find the work done by a particular force on an object is w equals f d cosine theta. Wnet kf ki k. The amount of energy transferred by a force is called the work done by that force.

Mgh 0 5 mv 2 f d k. For a constant torque the work can be expressed as and for a net torque newton s 2nd law for rotationgives. In other words the work done is equal to the change in energy. The work energy theorem states that the net work done by the forces on an object equals the change in its kinetic energy.

Work energy principle for angular quantities. The larger k is the stiffer the spring is and the harder the spring is to stretch. Pe ke w k. Mathematically it is expressed as.

Now to make it work you need to keep track of sign for each. In physics we can define energy as the capacity to do work. A horsepower is equal to 550 ft lb s and a kilowatt is 1000 watts. For example the work done against gravity is equal to the change in the potential energy of the body and the work done against all resistive forces is equal to the change in the total energy.

K is a measure of how difficult it is to stretch a spring. Integration of this power over the trajectory of the point of application c x t defines the work input to the system by the force. The rate of doing work is equal to the rate of using energy since the force transfers one unit of energy when it does one unit of work.