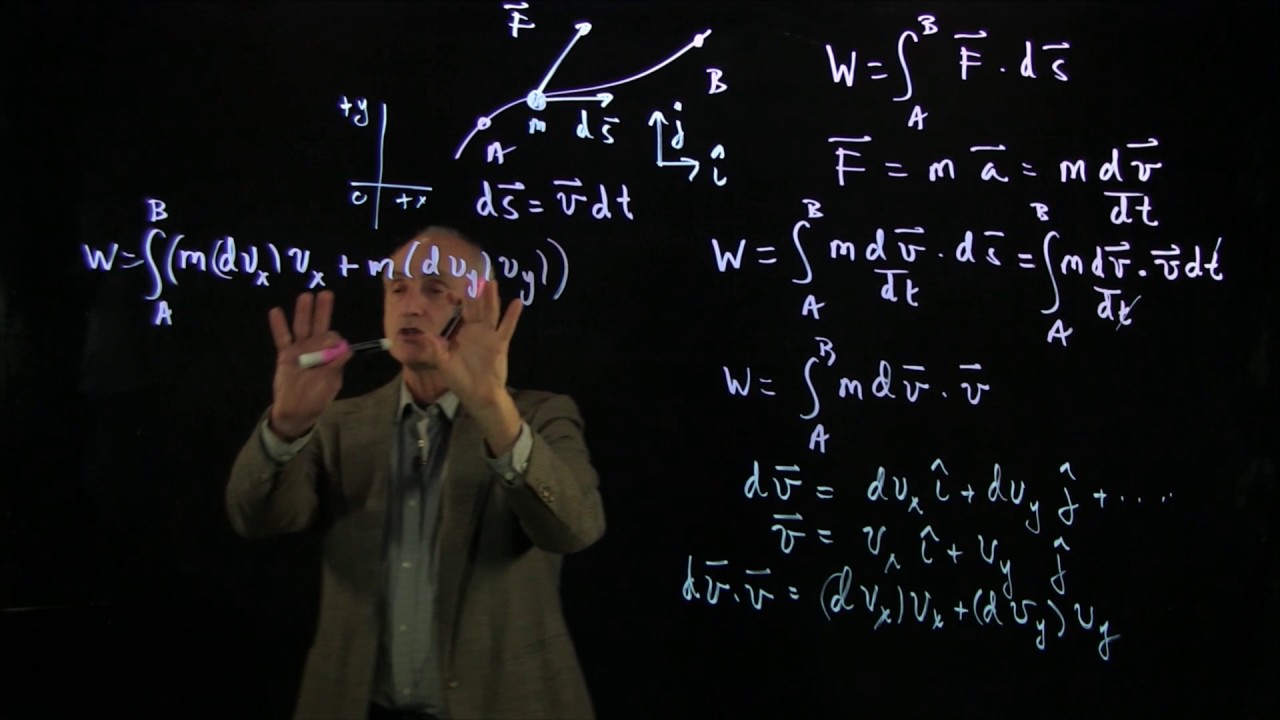Work Energy Theorem Formula Derivation

This is the derivation of work energy theorem. The work energy theorem is useful however for solving problems in which the net work is done on a particle by external forces is easily computed and in which we are interested in finding the particles speed at certain positions of even more significance is the work energy theorem as a starting point for a broad generalization of the concept. A variable force is what we encounter in our daily life.

wrought iron automatic gates melbourne wood frame storm windows work choice 5 shelf metal storage rack walmart world cup messi argentina jersey worn for flower carpet aj yamaha generator dealers in karachi woven landscape fabric uk wooden pencil door hanger

Work Energy Theorem Concept And Proof Youtube

Work Energy Theorem Variable Force Youtube

Work Energy Theorem Equation

How To State And Prove The Work Energy Theorem Quora

Work Energy Theorem Proof Hilz Media

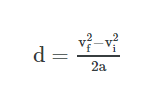
Work Energy Theorem Work Energy Power 2 In Hindi Youtube

For the sake of simplicity we will consider the.

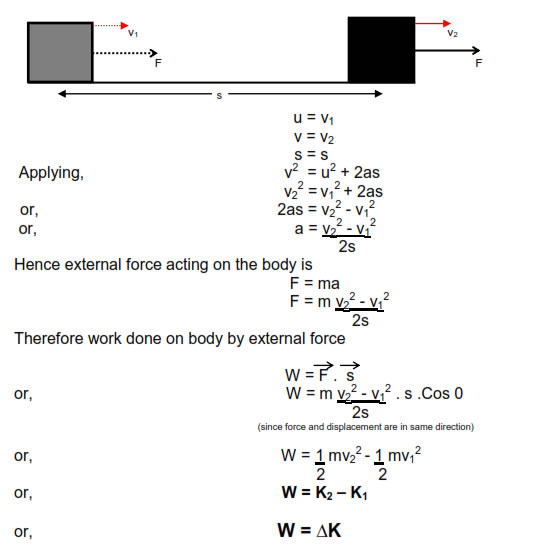
Work energy theorem formula derivation. The force that we come across everyday is usually variable forces. We will start with the definition of work and then apply newton s second law. Therefore we have proved the work energy theorem. The work energy theorem also known as the principle of work and kinetic energy states that the total work done by the sum of all the forces acting on a particle is equal to the change in the kinetic energy of that particle.

Deriving the work energy formula for variable force is a bit hectic. For any net force acting on a particle moving along any curvilinear path it can be demonstrated that its work equals the change in the kinetic energy of the particle by a simple derivation analogous to the equation above. Derivation of the work kinetic energy theorem for a single particle. This explanation can be extended to rigid bodies by describing the work of rotational kinetic energy and torque.

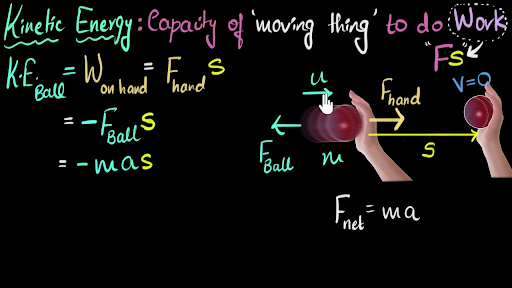
The work w done by the net force on a particle equals the change in the particle s kinetic energy ke. Work energy theorem for variable force. A constant force is rare in the everyday world. To develop a mathematical expression that relates work to the kinetic energy we ll assume that all of the work done on a system gives the system kinetic energy only.

The work done on an object is equal to the change in its kinetic energy. The derivation of the work energy theorem is provided here. Thus we can say that the work done on an object is equal to the change in the kinetic energy of the object. Latex text w delta text ke frac 1 2 text mv text f 2 frac 1 2 text mv text i 2 latex where v i and v f are the speeds of the particle before and after the application of force and m is the particle s mass.

Derivation of the mathematical expression for work kinetic energy theorem. The net work w done on a particle during a given time interval by the net force acting on the particle is equal to the change in the particle s kinetic energy during. Starting with the work energy theorem and then adding newton s second law of motion we can say that. Work kinetic energy theorem for a system of particles.

Workdone under a variable force. Proving the work energy theorem for a variable force is a little tricky. The kinetic energy derivation using only algebra is one of the best ways to understand the formula in depth. General derivation of the work energy theorem for a particle.

The work kinetic energy theorem for a single particle.